ML: Simple Math

Simply put, Machine Learning is about training a machine (model) to predict output for a given input.

Let us try to understand the math behind the prediction part.

Can you predict a missing number in the pattern below?

(1, 10)
(2, 20)
(3, 30)
(4, 40)
(5, ?)

That was quite simple. Try another one...

(0, 5)
(2, 3)
(6, -1)
(4, ?)

This one isn't that obvious. But there's a simple way. Let us treat these as (x,y) co-ordinates and try to plot a graph.

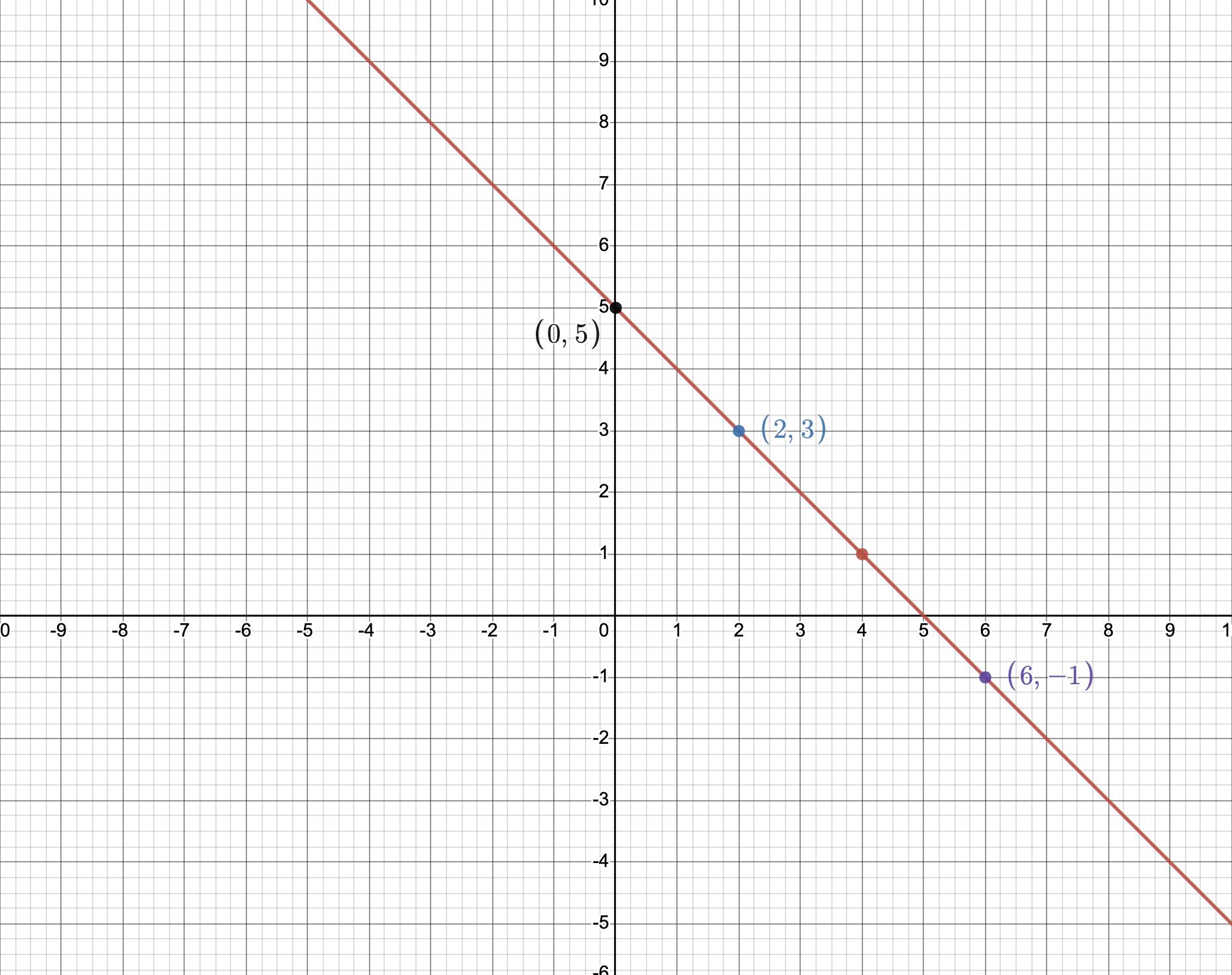
Now, were you able to find the missing number? Yes, it is 1 (the red dot).

Can we do it without a graph? The answer is a linear equation.

A linear equation is an algebraic equation where each term has an exponent of 1 and when this equation is graphed, it always results in a straight line. This is the reason why it is named a 'linear' equation.

The linear equation is given as -

y = mx + b

where,

m = slope (know more)

b = y-intercept (the point at which the line intersects the Y-axis) (know more)

Now, to find the value of y using the linear equation, for a given x we will need values of the slope m and the y-intercept b.

Consider the given points.

(x, y)
(0, 5)
(2, 3)
(6, -1)

Fortunately, we have a point with x = 0 so finding b, the y-intercept is easy.

Using the first point (x, y) = (0, 5) :

y = m * x + b
5 = m * 0 + b
5 = 0 + b
5 = b

we got b = 5.

---

Using b as 5 and the second point in the table (x, y) = (2, 3), let us find m, the slope.

y = m * x + b
3 = m * 2 + 5
3 - 5 = m * 2
-2 = m * 2
-2 / 2 = m
-1 = m

we got m = -1.

---

Let us use m = -1 and b = 5 to find the missing number.

(x, y)
(4, ?)

y = m * x + b
y = -1 * 4 + 5
y = -4 + 5
y = 1

We were finally able to find the missing number, 1.

---

In the next one, ML: Simple Model, we'll try to train a model to predict the value for the same example above.